LeetCode 62. 不同路径
题目描述
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
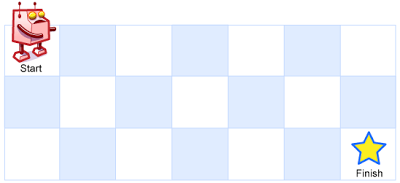
例如,上图是一个 7 x 3 的网格。有多少可能的路径?
示例 1:
javascript
输入: m = 3, n = 2
输出: 3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右
示例 2:
javascript
输入: (m = 7), (n = 3);
输出: 28;
提示: 1 <= m, n <= 100 题目数据保证答案小于等于 2 * 10 ^ 9
找出状态转移方程
找出重叠子问题,并且考虑规模: => 机器人从左上角到达第i行第j列一共有多少条路线?
js
dp(i, j) // 到达第i行第j列共有多少条路径
// 表示一般性的解: 机器人从左上角到达第1行第2列(这里索引从1开始)一共有多少条路线
dp(1, 2)
// 表示最终解: 机器人从左上角到达第m行第n列一共有多少条路线
dp(m - 1, n - 1)
js
dp(i, j) = dp(i - 1, j) + dp(i, j - 1)
dp(i - 1, j)中的i - 1表示上一行的相同列,j表示列相同dp(j - 1, i)表示行相同,列 -1
考虑特殊解:
- 往右直走 ->
只有一种走法 - 往下直走 (只走当前列列) ->
只有一种走法
即当 i===0 || j ===0
js
dp(i, j) = 1
js
const uniquePaths = function (m, n) {
const dp = (i, j) => {
if (i === 0 || j === 0) return 1
return dp(i - 1, j) + dp(i, j - 1)
}
return dp(m - 1, n - 1)
}
复制粘贴代码到力扣,提交代码,一气呵成,等待了十几秒,操!超时了!!!
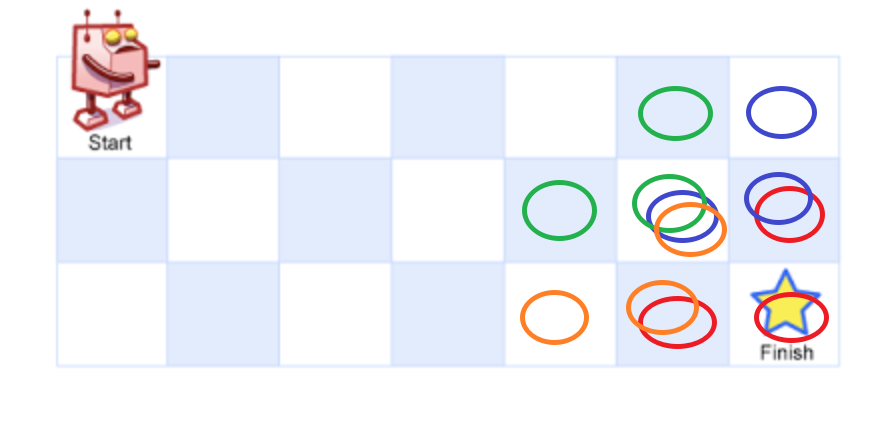
因为我们把求到达某个位置的不同路径拆分成了求该点顶部和左侧的不同路径和,即dp(i - 1, j) + dp(i, j - 1), 根据上图可以看到,我们遇到了很多的重复解, 很多位置我们重复计算了多次!
我们可以创建一个dp表,用于缓存已经求过的位置。
js
const uniquePaths = function (m, n) {
const cache = {}
const dp = (i, j) => {
if (i === 0 || j === 0) return 1
const key = `${i}-${j}`
if (cache[key]) return cache[key]
else
return cache[key] = dp(i - 1, j) + dp(i, j - 1)
}
return dp(m - 1, n - 1)
}
上面使用的是递归的解法,虽然递归解法的效率稍微会偏低一点,不过呢代码非常好理解,非常契合我们写出来的状态转移方程。
使用循环的解法
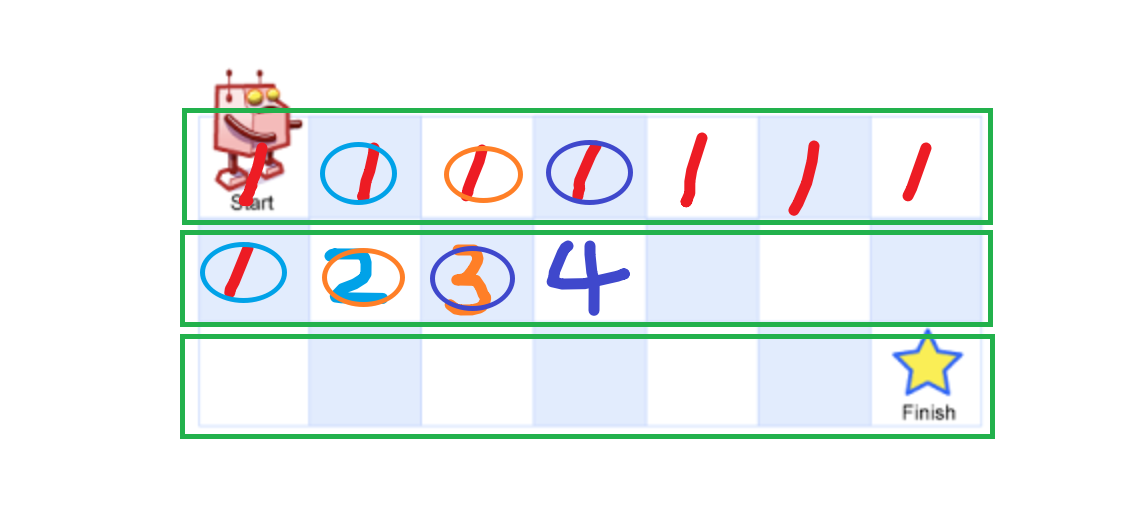
js
const uniquePaths = function (m, n) {
// 准备一张二维码的dp表
const dp = []
for (let i = 0; i < m; i++) {
dp.push([])
for (let j = 0; j < n; j++) {
if (i === 0 || j === 0)
dp[i][j] = 1
else
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
}
}
return dp[m - 1][n - 1]
}
解题思路
机器人只能向右或向下移动一步,那么当前路径数等于左边路径数+上边路径数之和,不过初始化第 0 行和第 0 列路径数都为 1。
javascript
/**
* @param {number} m
* @param {number} n
* @return {number}
*/
var uniquePaths = function (m, n) {
let dp = new Array(m);
// 初始化 第0行和第0列路径数都为1
for (let i = 0; i < m; i++) {
dp[i] = new Array(n);
dp[i][0] = 1;
}
for (let i = 0; i < n; i++) {
dp[0][i] = 1;
}
// 当前路径数等于左边路径数+上边路径数之和
for (let i = 1; i < m; i++) {
for (let j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
};
有了上面的解题思路,我们趁热打铁来搞定力扣上64.最小路径和