LeetCode 1219. 黄金矿工
题目描述
你要开发一座金矿,地质勘测学家已经探明了这座金矿中的资源分布,并用大小为 m * n 的网格 grid 进行了标注。每个单元格中的整数就表示这一单元格中的黄金数量;如果该单元格是空的,那么就是 0。
为了使收益最大化,矿工需要按以下规则来开采黄金:
每当矿工进入一个单元,就会收集该单元格中的所有黄金。矿工每次可以从当前位置向上下左右四个方向走。每个单元格只能被开采(进入)一次。不得开采(进入)黄金数目为 0 的单元格。矿工可以从网格中 任意一个 有黄金的单元格出发或者是停止。
示例 1:
javascript
输入:grid = [[0,6,0],[5,8,7],[0,9,0]]
输出:24
解释:
[[0,6,0],
[5,8,7],
[0,9,0]]
一种收集最多黄金的路线是:9 -> 8 -> 7。
示例 2:
javascript
输入:grid = [[1,0,7],[2,0,6],[3,4,5],[0,3,0],[9,0,20]]
输出:28
解释:
[[1,0,7],
[2,0,6],
[3,4,5],
[0,3,0],
[9,0,20]]
一种收集最多黄金的路线是:1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7。
提示:
javascript
1 <= grid.length, grid[i].length <= 15
0 <= grid[i][j] <= 100
最多 25 个单元格中有黄金。
来源:力扣(LeetCode)链接:https://leetcode-cn.com/problems/path-with-maximum-gold 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路
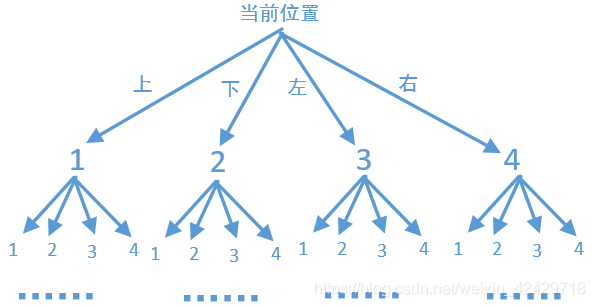
这题也是搜索相关,四个方向,不允许重复,不过这次我们需要从不同起点搜索,而且为了减少搜索次数,我们得从黄金数量不为 0 的点开始搜。然后每当走不下去的时候,就比较一下当前黄金数量,求出最大值即可。
javascript
/**
* @param {number[][]} grid
* @return {number}
*/
var getMaximumGold = function (grid) {
if (!grid || !grid.length) return 0;
let vis = [];
// 最终收集的最多黄金数量
let maxGold = 0;
for (let i = 0; i < grid.length; i++) vis[i] = [];
// 剪枝条件
let check = (x, y) => {
if (x < 0 || x >= grid.length || y < 0 || y >= grid[0].length || vis[x][y] === 1 || !grid[x][y])
return false;
return true;
};
let dfs = (x, y, total) => {
if (check(x, y)) {
vis[x][y] = 1; //防止重复
dfs(x + 1, y, total + grid[x][y]); // 四个方向搜索
dfs(x, y + 1, total + grid[x][y]);
dfs(x - 1, y, total + grid[x][y]);
dfs(x, y - 1, total + grid[x][y]);
vis[x][y] = 0;
} else {
// 走到底了,就比较一下当前黄金数量
maxGold = Math.max(maxGold, total);
}
};
// 起点从非0单元格开始
for (let i = 0; i < grid.length; i++) {
for (let j = 0; j < grid[0].length; j++) {
if (grid[i][j]) {
dfs(i, j, 0);
}
}
}
return maxGold;
};
cpp
class Solution {
public:
int getMaximumGold(vector<vector<int>>& grid) {
if (grid.empty() || grid[0].empty()) return 0;
int m = grid.size(), n = grid[0].size();
vector<vector<int>> vis(m, vector<int>(n, 0));
int maxGold = 0;
function<bool(int, int)> check = [&](int x, int y) {
if (x < 0 || x >= m || y < 0 || y >= n || vis[x][y] || !grid[x][y]) return false;
return true;
};
function<void(int, int, int)> dfs = [&](int x, int y, int total) {
if (check(x, y)) {
vis[x][y] = 1;
dfs(x + 1, y, total + grid[x][y]);
dfs(x, y + 1, total + grid[x][y]);
dfs(x - 1, y, total + grid[x][y]);
dfs(x, y - 1, total + grid[x][y]);
vis[x][y] = 0;
} else {
maxGold = max(maxGold, total);
}
};
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j]) {
dfs(i, j, 0);
}
}
}
return maxGold;
}
};
java
class Solution {
public int getMaximumGold(int[][] grid) {
if (grid == null || grid.length == 0) return 0;
int m = grid.length, n = grid[0].length;
int[][] vis = new int[m][n];
int maxGold = 0;
int[][] dirs = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};
// 剪枝条件
BiFunction<Integer, Integer, Boolean> check = (x, y) -> {
if (x < 0 || x >= m || y < 0 || y >= n || vis[x][y] == 1 || grid[x][y] == 0) return false;
return true;
};
// 搜索
BiConsumer<Integer, Integer> dfs = (x, y) -> {
if (check.apply(x, y)) {
vis[x][y] = 1;
for (int[] dir : dirs) {
dfs.accept(x + dir[0], y + dir[1]);
}
vis[x][y] = 0;
} else {
maxGold = Math.max(maxGold, grid[x][y]);
}
};
// 起点从非0单元格开始
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] != 0) {
dfs.accept(i, j);
}
}
}
return maxGold;
}
}
python
class Solution:
def getMaximumGold(self, grid: List[List[int]]) -> int:
if not grid or not grid[0]: return 0
m, n = len(grid), len(grid[0])
vis = [[0] * n for _ in range(m)]
maxGold = 0
dirs = [(1, 0), (0, 1), (-1, 0), (0, -1)]
# 剪枝条件
def check(x, y):
if x < 0 or x >= m or y < 0 or y >= n or vis[x][y] or grid[x][y] == 0: return False
return True
# 搜索
def dfs(x, y):
if check(x, y):
vis[x][y] = 1
for dir in dirs:
dfs(x + dir[0], y + dir[1])
vis[x][y] = 0
else:
nonlocal maxGold
maxGold = max(maxGold, grid[x][y])
# 起点从非0单元格开始
for i in range(m):
for j in range(n):
if grid[i][j] != 0:
dfs(i, j)
return maxGold
javascript
学如逆水行舟,不进则退